logistic与softmax推导

本文尝试从模型的基本假设出发，推导出模型假设，再利用最大似然推导出loss，最后进行梯度推导，详细梳理logistic与softmax。

广义线性模型

在进行推导模型之前，我们要说一下广义线性模型。广义线性模型有三点基本假设：
1、给定x下的y分布，由参数\(\theta\)控制；满足指数族分布，该指数族分布由参数\(\eta\)控制
2、模型的假设为y的期望
3、$\eta = \theta^{T}x$
那么什么是指数族分布呢？指数族分布由如下形式：
$p(y;\eta) = b(y) exp(\eta^{T}T(y)-a(\eta))$
那么如果一个分布我们可以将其表示为指数族分布，我们便可以通过广义线性模型的假设，推导得到模型。

logistic与伯努利分布

一、模型推导

在二分模型的时候，我们知道\(y \epsilon {0,1}\),很明显y是满足伯努利分布的，我们假设\(p(y=1) = \phi\),那么我们得到
$p(y) = \phi^{y}(1-\phi)^{1-y}$
那么该分布是指数族分布吗？我们可以尝试推导一下：
$p(y) = \phi^{y}(1-\phi)^{1-y}$
$= exp(ylog(\phi) + (1-y)log(1-\phi))$
$= exp(ylog(\frac{\phi}{1-\phi}) + log(1-\phi))$
明显这是一个指数族分布，我们有：
$b(y) = 1$
$T(y) = y$
$\eta = log(\frac{\phi}{1-\phi})$
$a(\eta) = -log(1-\phi)$
于是我们利用上面\(\eta\)与\(\phi\)的关系有:
$\phi = \frac{e^{\eta}}{1+e^{\eta}} = \frac{1}{1 + e^{-\eta}} \space (1)$
同时利用广义线性模型的假设，我们有:
$h_{\theta}(x) = E[y|x] = \phi$
$\phi = \frac{1}{1+e^{-\eta}} = \frac{1}{1 + e^{-\theta^{T}x}}$
我们可以得到： $h_{\theta}(x) = \frac{1}{1 + e^{-\theta^{T}x}} = p(y=1) \space (2)$
可以看到我们通过广义线性模型的推导，得到了伯努利分布的模型假设，即logistic的模型假设。(1)叫做sigmoid函数，其取值区间在(0,1)之前，函数图

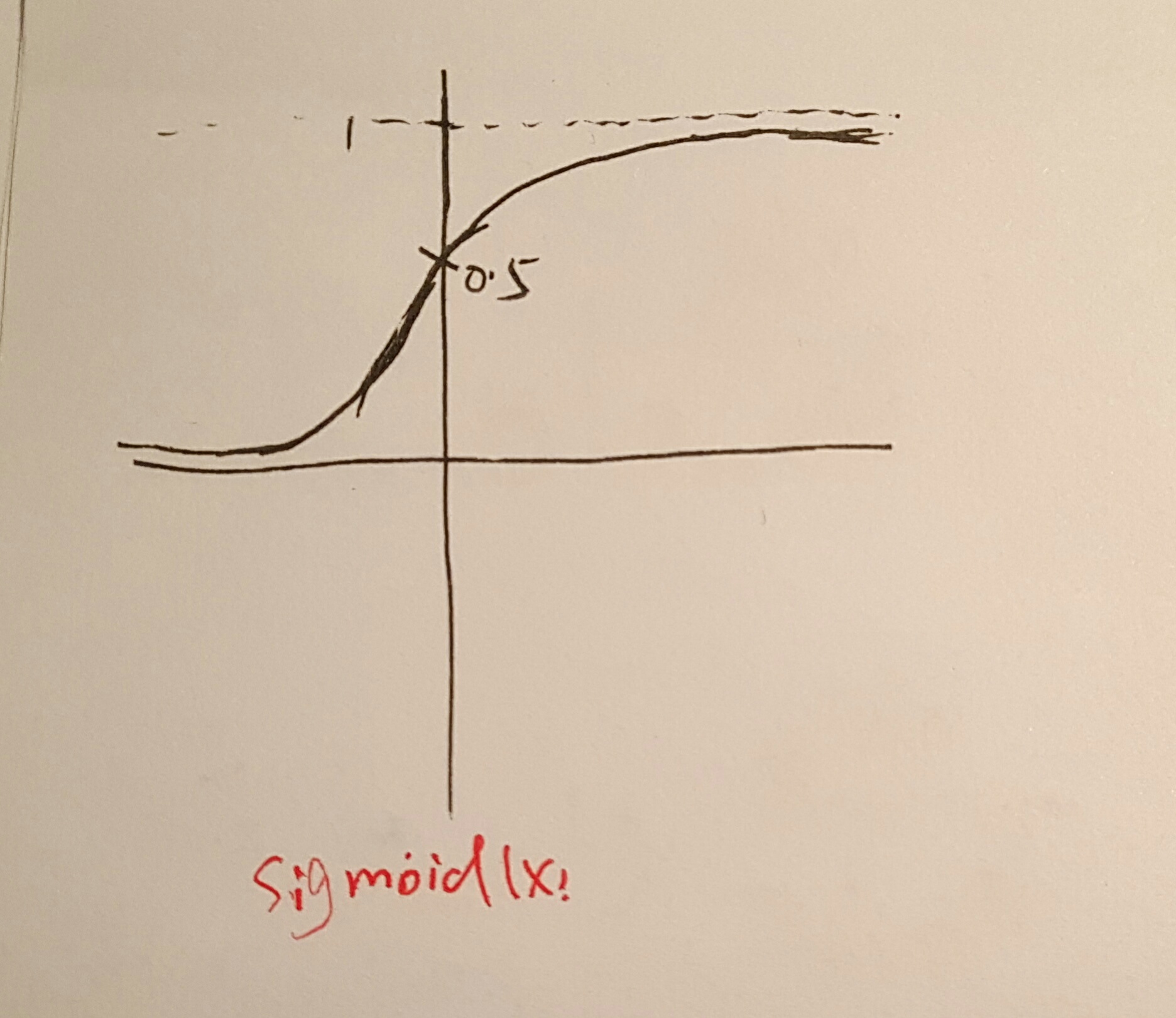
函数在0附近的梯度较大，但在离0较远处时梯度迅速下降，接近饱和。

二、loss推导

loss的函数定义有很多种，比如\(|y^{\star} - y|^{2}\)，但是对于sigmoid等含exp的假设来说是不适合的，该损失函数会随着sigmoid的饱和而跟随着饱和，因为:
$\frac{\partial L}{\partial x} = 2 \times (y^{\star} - y)$
可以看到每当\(y^{\star}\)饱和时，损失函数的梯度也会跟着饱和。对于这类假设来说最自然的是利用负log似然，即：
$L = -log(p(y|x)) = -(ylog(\phi)+(1-y)log(1-\phi))$
其中\(\phi = \sigma(\theta^{T}x)\),为了更好的说明-log能一定程度上抵消饱和效果，我们将上述损失函数进行一下改写，令\(z=\theta^{T}x\),那么有：
$p(y|x) = \frac{exp(yz)}{\sum_{y^{'}exp(y^{'}z)}}$
$=\frac{1}{1 + exp((1-2y)z)}$
$=\sigma((1-2y)z)$
我们将其带回到损失函数里有：
$L = -log(p(y|x)) = -log(\sigma((1-2y)z)) = \delta((1-2y)z)$
我们把函数\(\delta(x) = log(1 + e^{x})\)叫做softplus函数，函数图如下所示：

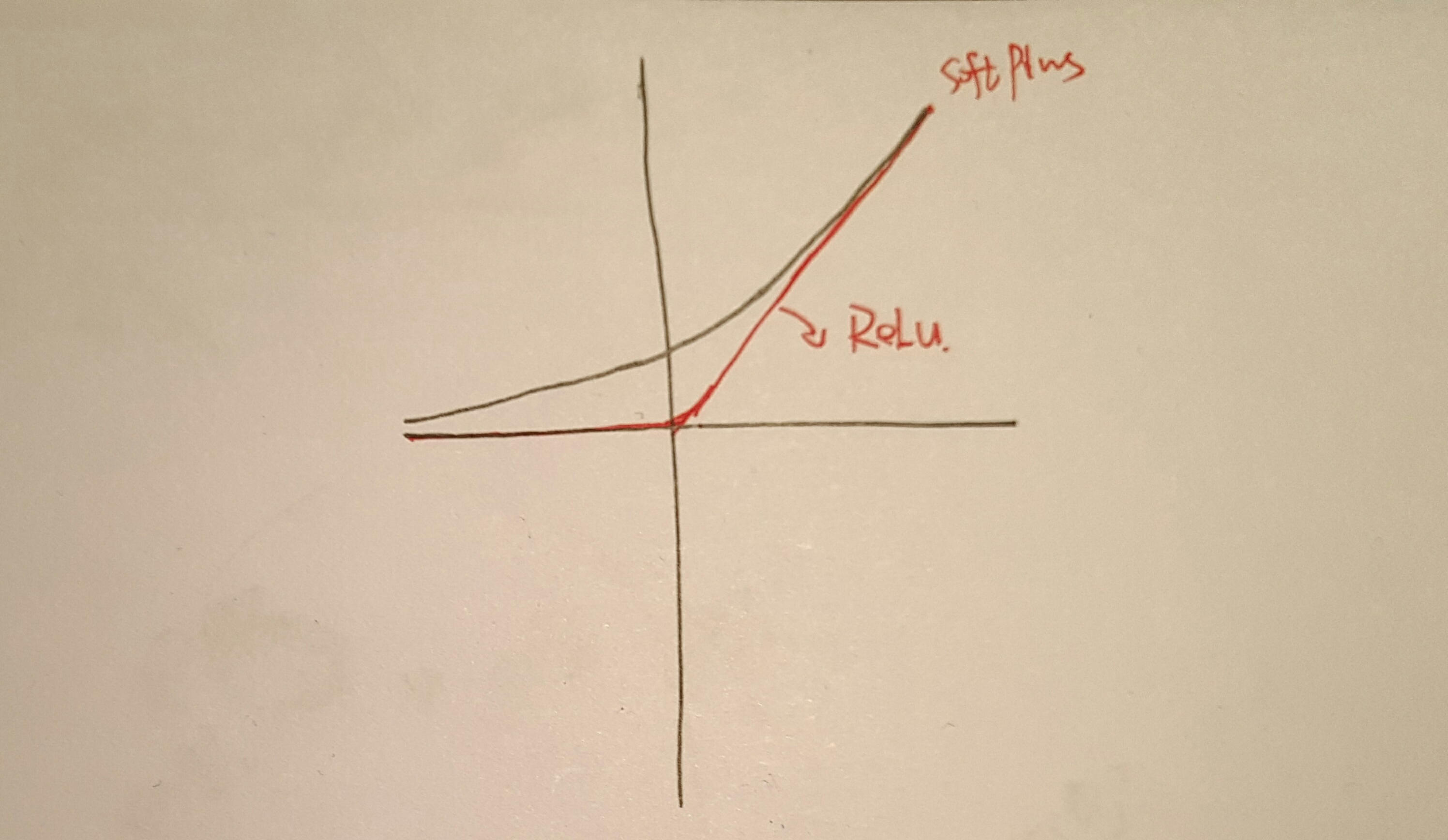
可以看到只有在\((1-2y)z\)为很大的负数时，梯度才会饱和，而此时我们其实已经得到正确答案了(y=0时,z为很小的负数;y=1时，z为很大的正数)；在我们错得较多时，梯度绝对值近似为1，有利于学习；可以看到利用了log的损失函数，我们能得到比较理想的梯度，而softplus其实可以看做是\(ReLU=max(0,x)\)的一个柔和近似版本。有了上面的总结，我们将其推广到数据集上，于是有了logistic的损失函数:
$L = -\frac{1}{m}\sum_{i} L_{i}$
$= -\frac{1}{m}\sum_{i}(y_{i}log(h_{\theta}(x_{i})) + (1-y_{i})log(1-h_{\theta}(x_{i}))))$
其中\(h_{\theta}(x)\)为(2)所示的函数。

三、梯度推导

求导很简单，我们先对sigmoid函数求一下导数，有:
$\frac{\partial \sigma(x)}{\partial x} = \frac{e^{-x}}{(1+e^{-x})^2} = \sigma(x)(1-\sigma(x))$
现在我们来对Loss求导，我们选择其中一项\(x_{i}\)求导，最终累加起来即可。
$\frac{\partial L_{i}}{\partial \theta} = -(y \frac{1}{\sigma(z_i)} -(1-y_i)\frac{1}{1-\sigma(z_i)})\sigma(z)(1-\sigma(z_i))\frac{\partial z_i}{\partial \theta}$
$=(\sigma(z_i)-y_i)x_i = (h_{\theta}(x_i) - y_i)x_i$
所以我们得到整体loss的梯度为：
$\frac{\partial L}{\partial \theta} = \frac{1}{m}\sum_i(h_{\theta}(x_i) - y_i)x_i$
利用梯度下降等方法优化时带入即可。

softmax与多项式分布

我们知道y可以取多个值，此时y满足的是多项式分布，假设y可以取k个值，那么它实际是被k-1个参数控制的，因为我们k个参数加起来为1。我们有:
$\phi_k = 1 - \sum_{i}^{k-1}\phi_i$
为了方便推导，我们先做一个预处理，令：
$T[1]=\begin{vmatrix} 1 \\0 \\.\\.\\0\end{vmatrix}$
$...$
$T[k-1] = \begin{vmatrix} 0 \\0 \\.\\.\\1\end{vmatrix}$
$T[k] = \begin{vmatrix} 0 \\0 \\.\\.\\0\end{vmatrix}$
即令\(T[y]_i = 1(y=i)\),并且有\(E[T[y]_i] = p(y=i) = \phi_i\)

一、模型推导

我们将多项式分布的表达写出有：
$p(y;\phi) = \phi_{1}^{y=1}\phi_{2}^{y=2}\cdot \cdot \phi_{k-1}^{y=k-1}\phi_{k}^{1-\sum_{i=1}^{k-1}\phi_i}$
$= exp(T[y]_1log(\phi_1)+T[y]_2log(\phi_2)+\cdot\cdot\cdot+(1-\sum_{i=1}^{k-1}T[y]_i)log(\phi_k))$
$= exp(T[y]_1log(\frac{\phi_1}{\phi_k}) + \cdot\cdot\cdot + log(\phi_k))$
对比指数族分布，我们可以得到：
$T[y] = T[y]$
$\eta_i = log(\frac{\phi_i}{\phi_k})$
$a(\eta) = -log(\phi_k)$
$b(y) = 1$
于是我们有：
$e^{\eta_i} = \frac{\phi_i}{\phi_k}$
$\phi_i = e^{\eta_i}\phi_i$
$1 = \phi_k\sum_{i=1}^{k}e^{\eta_i}$
于是我们得到了：
$\phi_k = \frac{1}{\sum_{i=1}^{k}e^{\eta_i}}$
利用广义线性模型的假设，我们带入有：
$\phi_i = \phi_k e^{\eta_i} = \frac{e^{\theta_{i}^{T}x}}{\sum_{j=1}^{k}e^{\theta_{j}^{T}x}}$
注意上面式子只试用到k-1，我们对于\(\phi_k\)则是上面那个公式。事实上在实际应用中我们并不将\(\phi_k\)加以区别对待，而是将其也用上述式子描述，不过我们会加以正则项等以控制模型参数。这也是我们常说softmax有个多余参数的原因，因为实际上我们只有k-1个自由参数。

二、loss推导

同样利用负log似然得到损失函数，对于一个例子我们有: $L_{i} = -log(p(y_i|x)) = -log( \phi_1^{y_i=1}\phi_2^{y_i=2}\cdot\cdot\cdot\phi_k^{y_i=k})$ $= -\sum_{j=1}^{k}1\{y_i=j\}log(\phi_j)$
上式看上去有点复杂，其实我们可以将求和省略，因为\(y_i\)只会有一个确切的值，于是我们有：
$L_{i} = -log(\phi_{y_i}) = -log(p(y_i))$
于是我们得到整体的损失函数为：
$L = \frac{1}{m}\sum_{i=1}^{m}L_i = -\frac{1}{m}\sum_{i=1}^{m}log(p(y_i))$
我们将模型假设带入有： $L = -\frac{1}{m}\sum_{i=1}^{m}log(\frac{e^{\theta_{y_i}^{T}x}}{\sum_{j=1}^{k}e^{\theta_{j}^{T}x}})$
通过最小负log似然我们得到了模型假设。

三、梯度推导

同样我们进行导数的推导,对于\(\theta_j\)的求导我们分为两种情况来讨论,一种情况是\(y_i \neq j\)另一种情况是\(y_i = j\)。为了书写方便，我们做一个简化，令\(\sum=\sum_{j=1}^{k}e^{\theta_j^{T}x}\). 于是对于某个数据点i,对于第一种情况我们有：
$\frac{\partial L_i}{\theta_j} = - \frac{\sum}{e^{\theta_{y_i}^{T}x_i}} \frac{-e^{\theta_{y_i}^{T}x_i}e^{\theta_j^{T}x_i}}{\sum^{2}}x_i$
$=-\frac{e^{\theta_j^{T}x_i}}{\sum}x_i = -p(y=j|x)x_i$
对于第二种情况，我们有：
$\frac{\partial L_i}{\partial \theta_j} = - \frac{\sum}{e^{\theta_{y_i}^{T}x_i}} \frac{e^{\theta_{y_i}^{T}x_i}\sum-e^{\theta_{y_i}^{T}x}e^{\theta_{y_i}^{T}x_i}}{\sum^{2}}x_i$
$= -(1 - \frac{e^{\theta_j^{T}x_i}}{\sum})x_i = -(1-p(y=y_i|x))$
我们将上述两式结合起来有： $\frac{\partial L_i}{\partial \theta_j} = -(1\{y_i=j\}-p(y=j|x))x_i$
于是我们得到了整体的loss函数为： $\frac{\partial L}{\partial \theta_j} = -\frac{1}{m}\sum_{i=1}^{m}\{1\{y_i=j\}- p(y=j|x;\theta)\}x_i$
可以看到softmax的推导虽然稍显复杂，但是仔细的数学推导还是可以得到最终的结果。