浅谈机器学习中的凸优化(下)---Lagrange duality

Nov.07-2016

本文紧接着上一篇讲机器学习中的凸优化问题。上一篇引进了凸集，凸函数以及凸优化的概念，并简单列举了它们的一些性质。本文将继续上文的工作，进一步引入凸优化理论中一个非常有用的概念拉格朗日对偶(Lagrange duality)，它在众多凸优化问题的求解中具有关键性作用，特别是对于SVM核方法的引入扮演着关键角色。

首先引入拉格朗日乘数(Lagrangian)，它是拉格朗日对偶(Lagrange duality)的基础；然后会引入原始问题(primal problems)以及对偶问题(dual problems)，紧接着会描述KKT条件(KKT condition)，它是原始问题和对偶问题对等的充要条件；最后会对原始对偶问题做一个直观上的解释。

读者可能会有疑问，为什么要引入原始问题与对偶问题呢？这是因为在有些情况下原始问题的求解十分困难，通过将其转换成对偶问题，很可能就能容易的求解该问题。我们都知道对于一个可导函数$f(x)$来说，$x^{\ast}$为全局最优的充要条件是$\bigtriangledown_{x}f(x^{\ast}) = 0$。但是对于一些有约束条件的凸优化问题来说，这种方法就不起作用了，因为$x^{\ast}$可能并不满足约束。对偶理论的提出可以对凸优化问题的最优解进行严格的数学推断。

首先我们引入带有约束的最优化问题的一般定义，该定义在上一讲中已经出现过

$minimize f(x)$
subject to $g_{i}(x) \leq 0, i=1,...,m$ （OPT)
$h_{i}(x) = 0, i=1,...,p$

其中$x \epsilon R^{n}$叫做优化变量(optimal variable)， $ f ： R^{n}\rightarrow R $以及$g_{i} : R^{n} \rightarrow R$都是可导的凸函数，$h_{i} : R^{n} \rightarrow R$为仿射函数。对这些概念还不太熟悉的话可以先回顾一下上一篇文章。

一、拉格朗日函数(Lagrangian)

首先引入拉格朗日乘数，它是拉格朗日对偶理论的基础。给定一个(OPT)形式的凸优化问题，广义的拉格朗日乘数是一个函数$\ L: R^{n} \times R^{m} \times R^{p} \rightarrow R$，定义为：

$\ L(x,\alpha,\beta) = f(x) + \sum_{i=1}^{m}\alpha_{i}g_{i}(x) + \sum_{i=1}^{p}\beta_{i}h_{i}(x)$

上式中有三个变量，其中$x$称作Lagrangian的原始变量(primal variables)，$\alpha, \beta$称作对偶变量(dual variables)或者拉格朗日乘子(Lagrange multipliers)。

我们可以将拉格朗日函数当做是(OPT)问题的一个修改版本，它将原问题中的限制条件隐性的考虑进了函数当中，后面我们将详细地讨论这些隐性条件，它使得两个问题完全对等起来。一个关于拉格朗日对偶理论背后关键理解是：对于任意凸优化问题，总存在一些对偶变量，它们使得不含限制条件的拉格朗日函数关于$x$求取的最小值与原始包含限制条件的最优化问题(OPT)的最小值联系起来。

二、原始问题与对偶问题(primal and dual problem)

为了阐述拉格朗日函数与最初形式的凸优化问题(OPT)间的联系，这里引入拉格朗日函数的原始问题与对偶问题。

a、原始问题(primal problem)

原始问题的定义为

$min_x\begin{bmatrix}max_{\alpha,\beta:\alpha \geq 0,\forall i} \ L(x,\alpha,\beta)\end{bmatrix} = min_x \theta_p(x)$

在上式中，函数$\theta_p: R^{n} \rightarrow R$ 叫做原始目标(primal objective)，而右侧的不包含限制条件的最小化问题就是原始问题(primal problem)。当$g_i(x) \leq 0, i=1,…,m$以及$h_i(x)=0,i=1,…,p$条件满足时，我们就说$x \epsilon R^{n}$ 是原始可行(primal feasible)的(即$x$满足初始最优化问题中的限制条件)。我们用$x^{\ast}$表示该问题的解，$p^{\ast}$表示原始优化目标此时取得的最优值。

下面我们来证明原始优化问题其实与最初的凸优化问题是等价的。将原始目标按照定义写出来：

$\theta_p(x) = max_{\alpha,\beta:\alpha_i \geq 0, \forall i} \ L(x,\alpha,\beta)$ $=max_{\alpha,\beta:\alpha_i \geq 0,\forall i} \begin{bmatrix} f(x) + \sum_{i=1}^{m}\alpha_i g_i(x) + \sum_{i=1}^{p}\beta_ih_i(x)\end{bmatrix}$ $=f(x) + max_{\alpha,\beta:\alpha_i \geq 0,\forall i} \begin{bmatrix} \sum_{i=1}^{m}\alpha_i g_i(x) + \sum_{i=1}^{p}\beta_ih_i(x)\end{bmatrix}$

因为$f(x)$与$\alpha,\beta$无关所以可以将其单独拿出来。下面单独考虑后面一部分，注意到

.如果任意的$g_i(x) > 0$，那么该max 可以取得正无穷大，因为只需要使得对应于该$g_i(x)$的$\alpha$取无穷大即可。而如果任意$g_i(x) \leq 0$，$\alpha_i$ 的非负性意味着一个非正数与一个非负数的和的最大值为0。

.同理，如果$h_i(x) \neq 0$，那么通过使得对应$\beta_i$取相同符号的无穷数可使得该乘积无穷大。而如果$h_i(x) = 0$，那么该项将恒为0，与$\beta$取值无关。

综合上面两点我们可以得到，如果$ x$是原始可行(primal feasible)的，那么上述大括号里的最大值将为0，而如果任意条件得不到满足，则将取正无穷值。所以我们可以将原始目标重写为

$\theta_p(x) = f(x) + \left\{\begin{matrix} 0 \space \space \space if \space x \space is \space primal \space feasible\\ \infty \space if \space x \space is \space primal \space \space infeasible \end{matrix}\right.$

所以我们可以将该原始问题看作是最初优化问题(OPT) 的一个修改版本。唯一的区别在于对于不可行点($x$不满足限制条件)来说，原始问题有一个无穷大的目标值。

b、对偶问题(dual problem)

对偶问题的定义十分直观，将原始问题(primal problem)中的max与min进行交换，我们便得到了一个完全不同的优化问题。

$max_{\alpha,\beta:\alpha_i \geq 0, \forall i}\begin{bmatrix}min_{x}\ L(\alpha, \beta, x)\end{bmatrix} = max_{\alpha,\beta:\alpha_i \geq 0 ,\forall i}\theta_{D}(\alpha,\beta)$

我们将函数$\theta_{D}: R^{m} \times R^{p} \rightarrow R$称作对偶目标(dual objective)，右侧带限制条件的优化问题称作对偶问题。我们说$\alpha, \beta$是对偶可行(dual feasible)当$\alpha_i \geq 0, i=1,…,m$。类似的我们用$(\alpha^{\ast}, \beta^{\ast}) \epsilon R^{m} \times R^{p}$来表示该对偶问题的解，用$d^{\ast}=\theta_D(\alpha^{\ast},\beta^{\ast})$来表示对偶目标取得的最优值。

在这里可以将原始问题与对偶问题做一个直观的对比。对偶问题将原始问题的max与min进行对调，这也是对偶一词的来源。进行对调后变成了完全不同的两个问题。注意到原始问题是一个无限制问题，而对应的对偶问题则拥有限制，同时对应的定义空间也不相同了，但目标的最优值却都是实数。下面我们将来讨论这两个问题的联系。

引理1. 如果$\alpha, \beta$是可行的(feasible)那么, $\theta_{D}(\alpha,\beta) \leq p^{\ast}$

证明很容易，

$\theta_D(\alpha,\beta)=min_x\ L(\alpha,\beta,x)$
$\leq \ L(\alpha, \beta, x^{\ast})$ $= f(x^{\ast}) + \sum_{i=1}^{m}\alpha_i g_i(x^{\ast}) + \sum_{i=1}^{p}\beta_i h_i(x^{\ast})$ $\leq f(x^{\ast}) = p^{\ast}$

上述证明第一行利用了对偶目标的定义，第二行是显然的，因为对偶目标是对$x$ 取最小，第三行是利用了拉格朗日函数的定义。最后一行是因为$x^{\ast}$是原始可行的而$\alpha, \beta$又是对偶可行的，所以$f(x^{\ast})$后面两项的和为非正数，而我们之前已经在原始问题中得到$f(x^{\ast}) = p^{\ast}$，得证。其实直观上也很好理解，一个不严谨的考虑为原始问题是求取最大中的最小，而对偶问题是求取最小的最大，显然最大中的最小会大于等于最小中的最大。

由引理1我们可以得到对于所有的可行$\alpha, \beta$，都有$\theta_D(\alpha, \beta) \leq p^{\ast}$。而对偶问题的优化目标为寻求对偶目标的最大值，那么它的作用其实可以看做为$p^{\ast}$寻找一个最靠近的下界。

由上述推论我们引出了关于任意原始对偶优化问题的弱对偶性(weak duality)

引理2弱对偶性(weak duality). 对于任意成对的原始对偶优化问题，$d^{\ast} \leq p^{\ast}$

在一些情况下上述的小于等于可以变成等于号，又引出了强对偶性(strong duality)

引理3强对偶性(strong duality). 在满足一些条件的情况下，原始对偶优化问题有 $d^{\ast} = p^{\ast}$

存在着很多使得强对偶性得到满足的限制，其中最常用的一个叫做Slater’s condition:当存在$x$使得所有的不等式得到满足(即$g_i(x) < 0, i=1,…,m$)，就说该原始对偶问题是满足slater条件的，即$d^{\ast} = p^{\ast}$。其证明又会涉及到很多凸优化理论的知识，这里就不给出了。但是有一点可以记住，几乎所有的凸优化问题都满足slater条件，即它们的原始问题和对偶问题拥有相同的优化目标值。

c、KKT条件

将上述的推论结合起来我们便可以得到关于原始问题以及对偶问题的KKT条件。在正式给出该条件前，我们先引出一个互补松弛条件(complementary Slackness)。

引理4互补松弛条件(complementary Slackness). 如果强对偶性满足，那么有$\alpha_i^{\ast}g(x_i^{\ast}) = 0$ for each i = 1, …,m

证明，

$p^{\ast} = d^{\ast} = \theta_D(\alpha^{\ast},\beta^{\ast})=min_x\ L(\alpha^{\ast},\beta^{\ast},x)$
$\leq \ L(\alpha^{\ast}, \beta^{\ast}, x^{\ast})$
$= f(x^{\ast}) + \sum_{i=1}^{m}\alpha_i g_i(x^{\ast}) + \sum_{i=1}^{p}\beta_i h_i(x^{\ast})$
$\leq f(x^{\ast}) = p^{\ast}$

由于上式中取等，所以两个不等式都将取得等号，意味着有，

$\sum_{i=1}^{m}\alpha_i g_i(x^{\ast}) + \sum_{i=1}^{p}\beta_i h_i(x^{\ast}) = 0$

由于$\alpha_i^{\ast}$为非负，$g_i(x^{\ast})$为非正，$h_i(x^{\ast})$为零，要保证该项和为零就必须保证$\alpha_i^{\ast}g_i(x^{\ast})$为零，因为该项为小于等于零的，如果有某一项小于了零将没有大于零的式子来使得整个式子等于零。将该互补松弛条件重写，我们得到，

$\alpha^{\ast} > 0 \rightarrow g_i(x^{\ast})=0$
$g_i(x^{\ast}) < 0 \rightarrow \alpha_i = 0$

也就是说只有当$g_i(x^{\ast}) = 0$ 的时候对应的$\alpha_i^{\ast}$才会不取零，即只有这些点才对整体有贡献，我们将这个现象称为主动约束(active constraint)。在SVM当中，主动约束又被称为支持向量(support vectors)。这就可以理解SVM算法名称的来源了，同时也就能解释在 SVM中只有支持向量是重要的，而它们的数量相对于整体来说是很少的。

下面正式给出KKT条件(KKT conditions) 如果$x^{\ast} \epsilon R^{n}, \alpha^{\ast} \epsilon R^{m}, \beta^{\ast} \epsilon R^{p}$满足以下条件

1、(Primal feasibility) $g_i(x^{\ast}) \leq 0, i = 1,…,m $ and $h_i(x^{\ast}) = 0, i=1,…,p$
2、(Dual feasibility) $\alpha_i^{\ast} \geq 0, i=1,…,m$
3、(Complementary Slackness) $\alpha_i^{\ast}g_i(x^{\ast}) = 0, i = 1,…,m$
4、(Lagrangian stationarity) $\bigtriangledown_{x} \ L (x^{\ast}, \alpha^{\ast}, \beta^{\ast}) = 0.$

那么$x^{\ast}$是原始优化的解，$\alpha^{\ast}, \beta^{\ast}$是对偶优化的解。同时如果强对偶满足，那么原始优化的解和对偶优化的解必须满足上述的1-4。

d、原始对偶问题的直观概念

考察原始问题对等的原优化问题，由于我们已经得到$h_i(x)$不会对最终的优化结果造成影响，所以为了方便描述将该问题简化为，

$mininize \space f(x)$
$subject \space to \space g(x) \leq 0$

注意到上式中，$f(x), g(x): R^{n} \rightarrow R$。我们定义一个$R^{2}$ 中的集合G,

$G = {(y,z): y=g(x), z=f(x) \space for \space some \space x \epsilon X}$

那么该集合可以用下图来直观表示，
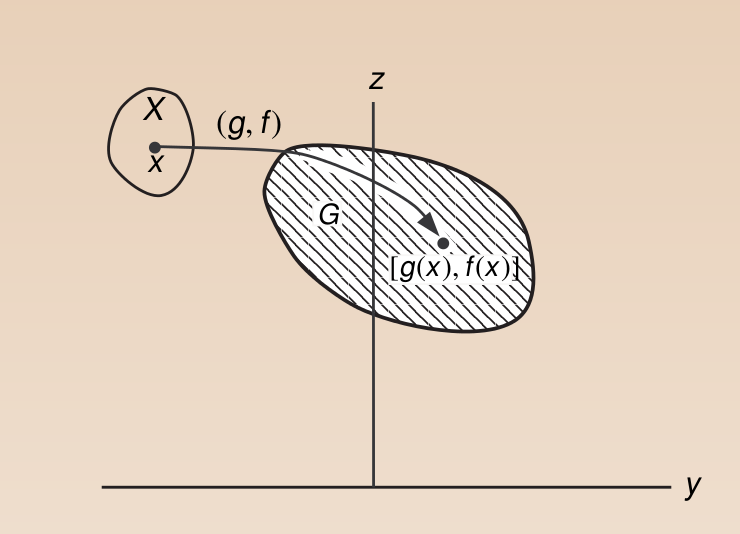primal $X$中的点经过映射$g,f$到了集合G当中，注意我们想要取得在$g(x) \leq 0$情况下$f(x)$的最小值，很显然该最优化点在图中可以很容易找到，
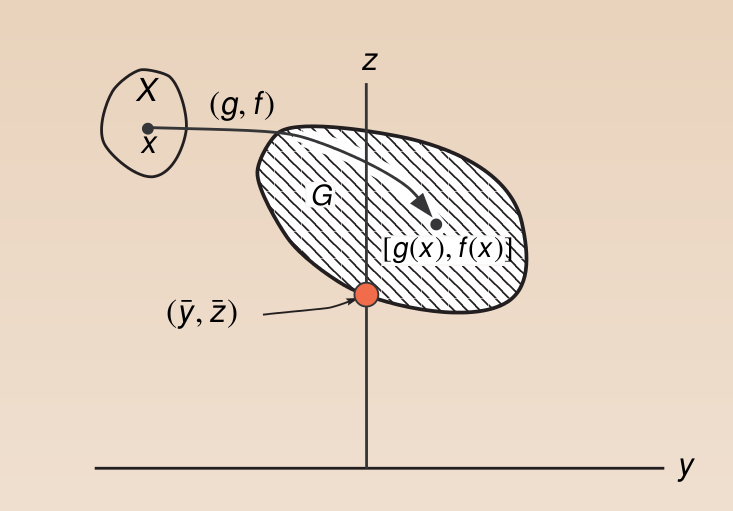primal_optimal 图中标红点即为我们找到的最优

下面来看对偶优化问题，

$maximize \space \theta(u)$
$subject \space to \space u \geq 0$

其中有

$\theta(u) = minimize(f(x) + ug(x):x\epsilon X)$

同样$x$ 经过映射到集合G，定义直线

$z + uy = \alpha$

在该直线我们知道，$-u$为直线的斜率，$\alpha$为该直线的截距。还是利用上面定义的集合G，我们有该问题的直观表示为，
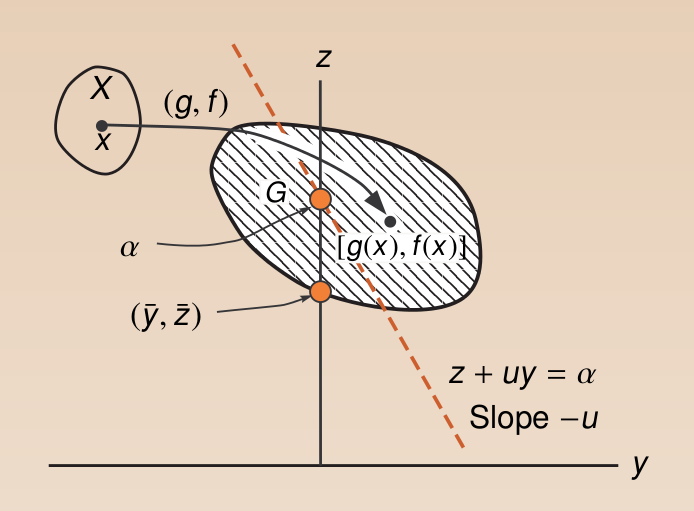dual 由于$u \leq 0$我们知道斜率始终是非正的，那么在固定$u$的情况下能得到的$\alpha$的最小为：将直线左移与集合G左边相切，得到最小截距。即$\theta(u)$为$\alpha$在固定$u$时能取到的最小值。如下所示，
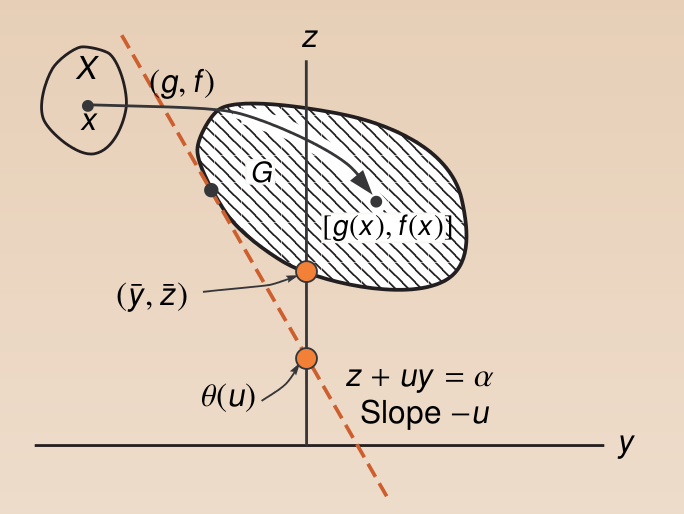dual_primitive 下面来考虑怎样将$\theta(u)$最大化，由前一步已经知道$\theta(u)$即一系列斜率为负，与集合G相切的直线的截距。寻找u的过程即为寻找一系列相切直线的过程。直观上很容易感受我们能够得到的最大值为当直线与0点相切的时候的截距，也即该切点，如下所示，
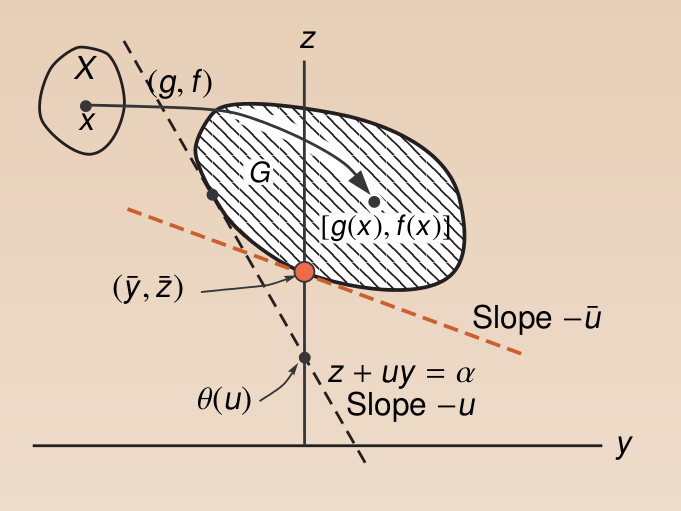dual_optimal 通过这个直观过程我们看到，虽然原始问题与对偶问题是两个完全不同的优化问题，但是它们在一定的条件下会拥有相同的解。有一点很重要，即集合G需要是一个凸集，从这里也能看到我们前面强调拉格朗日函数所构成需要为一个凸集的必要性。