浅谈机器学习中的凸优化(上)

机器学习中经常会碰到求解函数最优值的情况:给定一个从n维空间到1维空间的函数映射\(f(x):R^{n}->R\)，寻找一个\(x\)使得\(f(x)\)取得最小或最大值。比如线性回归，逻辑回归以及SVM等都可以归类到最优化框架问题里——我们根据某个概率分布得到一个假设和代价函数，然后利用优化算法寻找合适的参数，使得该代价函数取得全局最优值，得到最终的训练参数结果。

在一般情况下，想要寻找一个函数的全局最优是十分困难的，因为常见的优化算法比如梯度下降，牛顿法等多会在局部最优点收敛。但是对于一类叫做凸优化的特殊优化问题来说，在大多数情况下我们可以很高效的找到其全局最优结果，因为对于凸优化问题来说其局部最优即为全局最优，这一点将在后面给出证明。在机器学习中我们碰到的优化问题大多都是凸优化问题，特别是在SVM的推导中，凸优化起了至关重要的作用，想要深刻的理解SVM，对基本的凸优化理论了解必不可少。

本主题分上下两篇。第一篇主要探讨和引入凸优化问题；下篇将着重介绍凸优化中的拉格朗日对偶理论；它们对于理解SVM背后的原理必不可少。

一、凸集与凸函数

首先需要理解凸的概念，主要会涉及到凸集以及凸函数的定义。

a、凸集

凸集的定义：
一个集合C，\(x, y \epsilon C\)，以及0到１之间的任意实数\(\theta\), \(\theta x + (1-\theta)x \epsilonＣ\)，那么就说C是凸的。

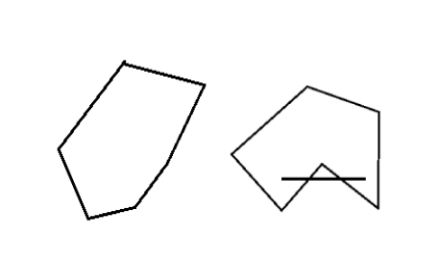
直观上来看即在集合中选任意两点，将其连线，连线上的所有点都属于该集合，则称该集合为凸集。值得注意的是，凸集的交仍然是凸集，所有半正定矩阵的集合也为一个凸集，感兴趣可以利用凸集的定义进行证明这里略过。

b、凸函数

凸函数的定义：
一个由n维空间到实数域的函数映射是凸(convex)的——如果其定义域为凸集，且对于\(x, y \epsilon D(f)\)，以及０到１之间的任意实数\(\theta\)满足

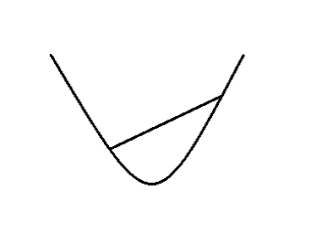
直观上来看即在函数图像上任选两个点，将它们连线，那么两点间的函数图像会在这条线以下。当\(\theta \neq 0, x \neq y \)，如果上述条件不能取等，那么就说\(f(x)\)是严格凸函数(strictly convex)。当\(-f(x)\)为凸的时候，我们说\(f(x)\)是凹(concave)的。

函数凸性判断:
函数的凸性判断除了利用定义外，最常利用的是一阶条件(first order condition for convexity)和二阶条件(second order condition for convexity)进行判断。

.一阶条件：如果\(f(x)\)一阶可导，那么\(f(x)\)为凸当且仅当其定义域D为凸，\(x, y \epsilon D(f)\)满足：\(f(y) \geq f(x) + \bigtriangledown f(x)^{T}(y-x)\)

直观上可以理解为在函数任意一点做切线，该切线上的任意值都会在函数下方。
.二阶条件：如果\(f(x)\)二阶可导，那么\(f(x)\)为凸当且仅当其定义域为凸，且其海森矩阵为半正定矩阵。
直观上可以理解为其斜率始终是在保持不变或者增长的。二阶判断条件应该是最常用到的判断条件，对函数二次求导判断其海森矩阵的正定性即可。

\(\alpha\)-sublevel set:
进一步由凸函数可以引入一个相当重要的凸集，\(\alpha\)-sublevel set。给定一个凸函数f，以及一个实数\(\alpha\), \(\alpha\)-sublevel set定义为：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　$\left \{ x \epsilon D(f): f(x) \leq \alpha \right \}$

即所有满足\(f(x) \leqslant \alpha\)的x所组成的集合。证明十分简单，考虑\(x, y \epsilon D(f)\)有\(f(x) \leqslant \alpha,f(y) \leq \alpha\).那么有：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　$f(\theta x + (1-\theta)y) \leq\theta f(x) + (1-\theta)f(y) \leq \theta \alpha + (1-\theta)\alpha = \alpha$

注意到此处如果小于符号取大于便不存在这个凸的性质了，\(\alpha\)-sublevel将会在之后的凸优化问题中用到。

常见凸函数:
下面给出一些凸函数的例子，它们在机器学习的优化中会经常出现。

.指数族函数：\(f(x)=e^{ax}\), \(a \epsilon R\). 利用二阶判断条件可以得到\({f(x)’’ = a^{2}e^{ax}}\), 其对于所有x都为非负，所以该海森矩阵为半正定矩阵，那么指数族函数即为凸的。

.仿射函数：\(f(x)=b^{T}x + c, b \epsilon R^{n}, a \epsilon R\).同理通过二阶判断条件我们能够得到对于所有的x, \( \bigtriangledown _{x}^{2}f(x) = 0\)。即该海森矩阵既是半正定的又是半负定的,意味着仿射函数既为凸函数也为凹函数，这一点十分重要将要在以后用到。

.二次函数：\(f(x)=\frac{1}{2}x^{T}Ax + b^{T}x + c, A \epsilon R^{n\times n}\)且为对称矩阵（关于这一点将会在以后的博文中给予说明，我们会看到Ａ的非对称部分对于整个式子将不存在贡献），\(b \epsilon R^{n},c \epsilon R\)。同样利用二次判定条件可以得到\(\bigtriangledown _{x}^{2}f(x)=A\)。那么二次函数的凸性便由Ａ决定，如果Ａ为半正定矩阵则二次函数为凸函数。注意特殊情况\( f(x)=|x|^{2} = x^{T}x \), 这时\(A=I, b=0, c=0\)。I为正定矩阵，所以该函数为严格凸函数。

.凸函数的非负加权和：假设\( f_{1},f_{2},…,f_{k} \)为凸函数，\(w_{1},w_{2},…,w_{k}\)为非负实数，那么\(f(x)=\sum_{i=1}^{k}w_{i}f_{i}(x)\)。在这里利用凸函数定义进行证明。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　$f(\theta x + (1-\theta)y) = \sum_{i=1}^{k}w_{i}f_{i}(\theta x + (1-\theta)y)$
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　$\leq \sum_{i=1}^{k}w_{i}(\theta f_{i}(x) + (1-\theta)f_{i}(y))$
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　$=\theta \sum_{i=1}^{k}w_{i}f_{i}(x) + (1-\theta)\sum_{i=1}^{k}w_{i}f_{i}(y)$
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　$=\theta f(x)+(1-\theta)f(y)$

得到最终证明。注意其中\(w_i \geq 0\)即非负很重要，她是第二步小于等号的关键。

二、凸优化问题

在讨论了那么多关于凸集以及凸函数的概念后，终于来到了机器学习我们熟悉的地方—-凸优化问题。

a、凸优化问题定义

凸优化形式化的一般定义为：

其中f(x)为凸函数，Ｃ为一个凸集, x为优化目标值。

当然上述写法并不直观，所以经常我们会采取另外一种形式来书写

$minimize f(x)$
subject to $g_{i}(x) \leq 0, i=1,...,m$
$h_i(x) = 0, i=1,...,p$

其中\(f\)为凸函数，\(g_{i}\)为凸函数，\(h_{i}\)为仿射函数, x为优化目标值

上述转化表达中有两点至关重要：
a、\(g_{i} \leq 0\),这里必须为小于等于符号，即\(g_{i}\)的０-sublevel集合，这样才能保证x的集合为凸集。(回忆\(\alpha\)-sublevel$里的证明)

b、\(h_{i}=0, h_{i}\)必须为仿射函数。直观上可以理解为\( h_{i} \leq 0 \) && \( h_{i} \geq 0 \)两个条件同时满足，也就是说\(h_{i}\)需要既为凸又为凹，那么根据二次判断条件，其海森矩阵需要为零矩阵。所以\(h_{i}\)需要为仿射函数。可以看到\(g_{i}\)和\(h_{i}\)的限制，将x限制到了一个凸集里。

为了方便后文描述这里引入符号\( p^{\ast} \)来表达该优化问题的最优值。即

当\( p^{\ast} \)不存在时，我们说该问题是不可优化的，当\( p^{\ast} \)可以取负无穷时，我们说该问题是无下界的。当\( f(x^{\ast}) = p^{\ast} \)时，我们说\(x^{\ast}\)为最优点*。

b、凸优化问题中的局部最优与全局最优

前面我们说过对于优化问题来说想要寻找其全局最优并不容易，但是对于凸优化问题来说我们往往能高效的找到其全局最优，这是因为对于凸函数来说其局部最优就是全局最优。要形式化的证明这一过程，首先给出局部最优和全局最优的定义。

局部最优与全局最优:
如果点\(x\)是可行的（满足凸优化问题的限制条件），且存在实数\(R > 0\), 对于所有满足\(\left || x-z \right ||_{2} \leq R \)的可行点\(z\), 都有\(f(x) \leq f(z)\),就称\(x\)为局部最优点.

如果点\(x\)是可行的，对于所有可行点\(z\)都有\(f(x) \leq f(z)\),则称\(x\)为全局最优点.

有一个非常重要的结论是：对于凸优化问题来说局部最优点即为全局最优点

下面给出证明：假设\(f(x)\)为局部最优值，\(f(y)\)为全局最优值，\(f(z)\)为局部范围\(R\)内的一点，那么有\(f(x) > f(y)\),\(f(x) < f(z)\)。假设

\(z = \theta y + (1-\theta)x, \theta = \frac{R}{2\left|x-y\right|_{2}} \)

先来看这一假设的合理性：

$\left \| x-z \right \|_{2} =$
$\left\|x - (\frac{R}{2\left \| x-y \right \|_{2}}y + (1-\frac{R}{2\left \| x-y\right \|})\right\|_{2}$
$= \left \|\frac{R}{2\left\|x-y\right\|_{2}}(x-y) \right\|_{2}$ $=R/2 < R$

说明假设合理，\(z\) 在范围R内，\(x\)的局部最优性满足。而另一方面，根据凸函数的性质有：

利用前面\(f(x) < f(y)\)的假设我们有，\(f(z) < f(x)\).然而这与另外一个假设\(f(x) < f(z)\)相矛盾，所以可以得到\(f(x)\)即为全局最优值。意味着对凸优化问题来说，如果我们找到一个局部最优值那么该局部最优即为全局最优。

本文有凸集，凸函数引入了机器学习中经常会遇到的凸优化问题，说明了其合理性。下一步将进一步讨论凸优化理论中非常重要的拉格朗日对偶问题，它对于SVM的引出至关重要。