浅谈优化方法与泰勒展开

Mar.26-2017

在机器学习中我们最常遇到的便是优化问题，而最常用的便是基于梯度的优化方法。本文首先尝试利用泰勒展开式说明梯度下降以及牛顿法的来源，然后再梳理一下深度学习中梯度下降法的一些变形。

梯度下降&牛顿法与泰勒展开

一个基本问题是我们要优化目标函数$f(\overrightarrow{w})$,但是我们对其了解并不多，应该怎样进行呢？一个关键技巧在于我们假设该函数在局部是一个简单函数，然后我们便可以优化简单函数来近似优化该函数，泰勒展开的引入就在于此。我们知道对于函数$f(\overrightarrow{w}+\overrightarrow{s})$有泰勒展开:

$f(\overrightarrow{w}+\overrightarrow{s}) = f(\overrightarrow{w}) + g(\overrightarrow{w})^{T}\overrightarrow{s} + \frac{1}{2}\overrightarrow{s}^{T}H(\overrightarrow{w})\overrightarrow{s} + ...$

这里$g(\overrightarrow{w})$表示$f(\overrightarrow{w})$的一阶梯度，$H(\overrightarrow{w})$表示$f(\overrightarrow{w})$的Hessian矩阵。我们假设$|\overrightarrow{s}|$很小，这样我们便有$\overrightarrow{w} + \overrightarrow{s}$接近于$\overrightarrow{w}$，在局部我们便可以得到函数近似表达，然后进行进一步的优化。接下来我们详细说说梯度下降和牛顿法。

一、梯度下降与泰勒一次逼近

梯度下降利用了函数的泰勒一阶展开，假设函数在局部是线性的，即:

$f(\overrightarrow{w}+\overrightarrow{s}) \approx f(\overrightarrow{w}) + g(\overrightarrow{w})^{T}\overrightarrow{s}$

那么想要求解左边的最小值便转换为了求解上式右边的最小值。也即求解$g(\overrightarrow{w})^{T}\overrightarrow{s}$最小，这其实便转换为了求解两个向量内积的最小值，我们知道两个向量相反时内积应该是最小的，所以我们便有:

$\overrightarrow{s} = -\alpha g(\overrightarrow{w})$

$\alpha$为一个标量参数，由我们自己设定，成为学习速率。这就是梯度下降法的来源，用直线去逼近函数的局部。每一步我们更新:

$\overrightarrow{w} = \overrightarrow{w} - \alpha g(\overrightarrow{w})$

其更新过程可以如下所示：
gd1
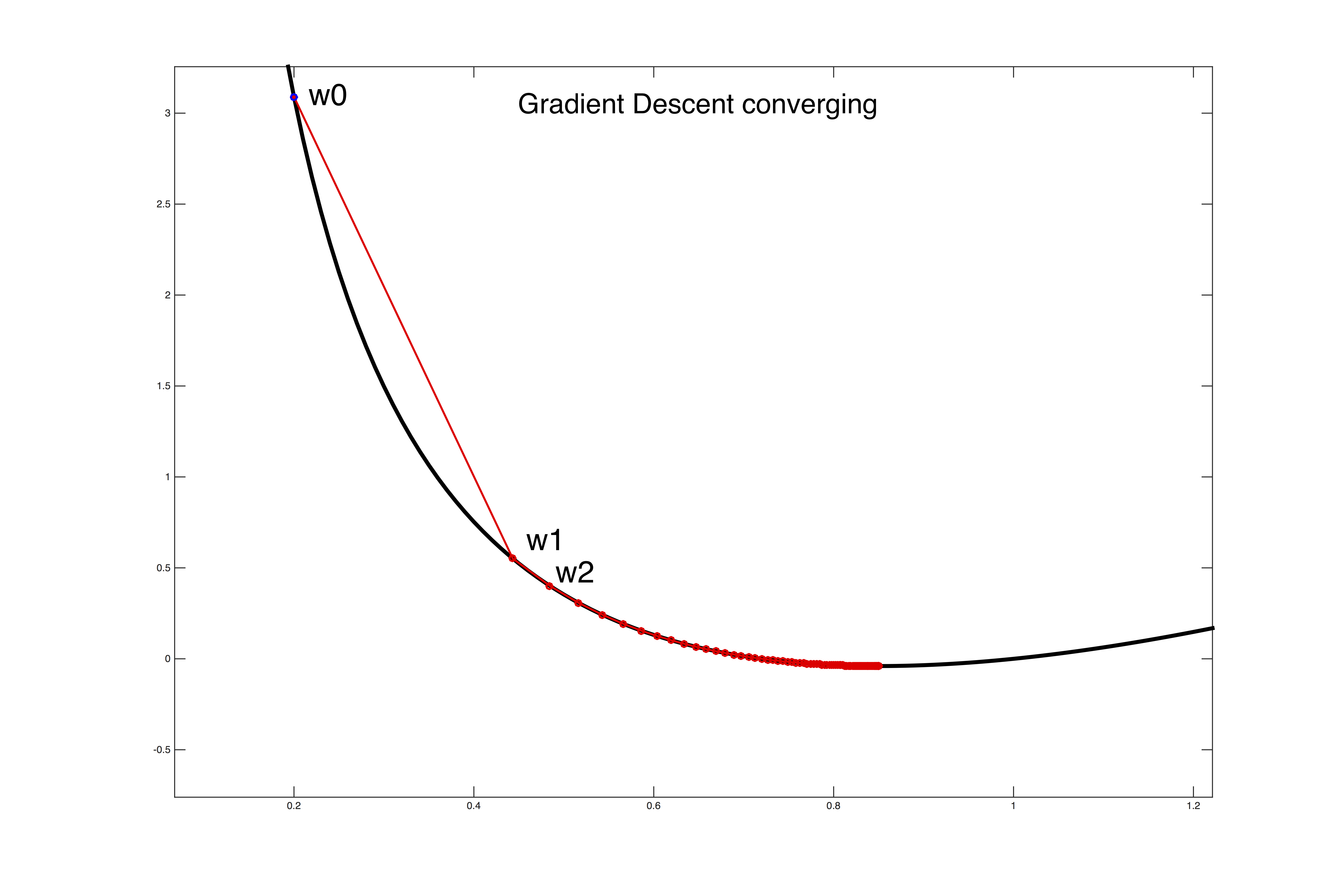
对于相同的$\alpha$，当梯度比较大时步子较大，当梯度较小时步子较小。但请注意我们的推导成立的条件是$|\overrightarrow{s}|$很小，这样一阶的泰勒展开才准确，所以$\alpha$的取值不能太大，如果太大的话会造成overshutting的问题，即如下所示:
gd2
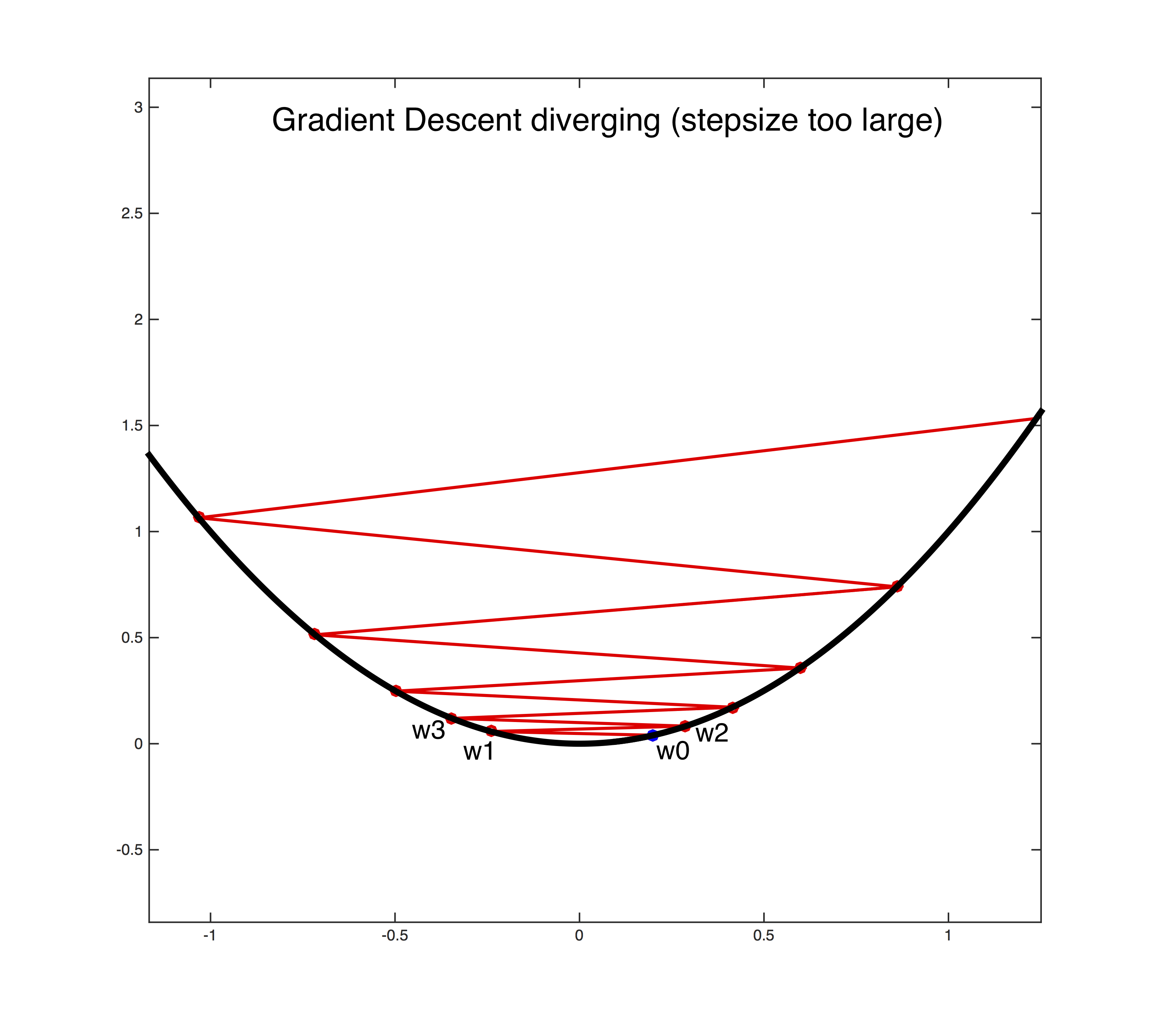
关于梯度下降的一些变形我们等下再讲，下面再来看看牛顿法。

二、牛顿法与泰勒二次逼近

相信大家已经想到了牛顿下降法利用的是泰勒的二阶展开，假设函数在局部是一个二次函数。即:

$f(\overrightarrow{w}+\overrightarrow{s}) \approx f(\overrightarrow{w}) + g(\overrightarrow{w})^{T}\overrightarrow{s} + \frac{1}{2}\overrightarrow{s}^{T}H(\overrightarrow{w})\overrightarrow{s}$

我们知道二次函数的Hessian矩阵一定是对称半正定的(可以参考我之前关于凸优化的博文)，所以这其实是一个局部的凸优化问题。同样的我们求解上式右边的最小值，即

$g(\overrightarrow{w})^{T}\overrightarrow{s} + \frac{1}{2}\overrightarrow{s}^{T}H(\overrightarrow{w})\overrightarrow{s}$

可以看到它是$\overrightarrow{s}$的一个二次函数，我们对$\overrightarrow{s}$求导，得到:

$g(\overrightarrow{w}) + H(\overrightarrow{w})\overrightarrow{s}$

令其等于0我们便得到了:

$\overrightarrow{s} = -\left [H(\overrightarrow{w})\right ]^{-1} g(\overrightarrow{w})$

于是我们便得到了牛顿法的更新规则，如上所示。
注意到牛顿法相比于梯度下降，是利用__二次函数__去进行局部逼近，不存在$\alpha$的设置问题，同时如果原来函数就是二次函数的话，牛顿法能够直接到达最低点而梯度下降法需要迭代，所以如果函数局部能够很好地被二次函数逼近的话，相比于梯度下降,牛顿法收敛会快很多。但是如果函数的局部非常平坦，那么用二次逼近后Hessian矩阵会有很多值接近于0，取逆后会非常大，造成非常大的步伐，此时优化过程便会发散了。牛顿法还有一个天然的缺陷是需要求Hessian矩阵的逆，如果$\overrightarrow{w}$的维度很高，那么求取代价是非常昂贵的；特别是在深度学习中，参数的个数经常上百万，求逆操作变得根本不可行，所以在深度学习中一般都是利用随机梯度下降法(SGD)以及其变形。

深度学习中常用的优化方法

深度学习的训练基本都是基于梯度的更新方法，然而直接不加修改的SGD方法存在着缺陷很少用，一个最直观的缺点是：每次更新是由主要的梯度方向锁控制的，如果函数曲面在某一个方向上波动很大的，整个更新过程便会不断地在大梯度方向上波动，而在小梯度方向缓慢前进。如下
sgd

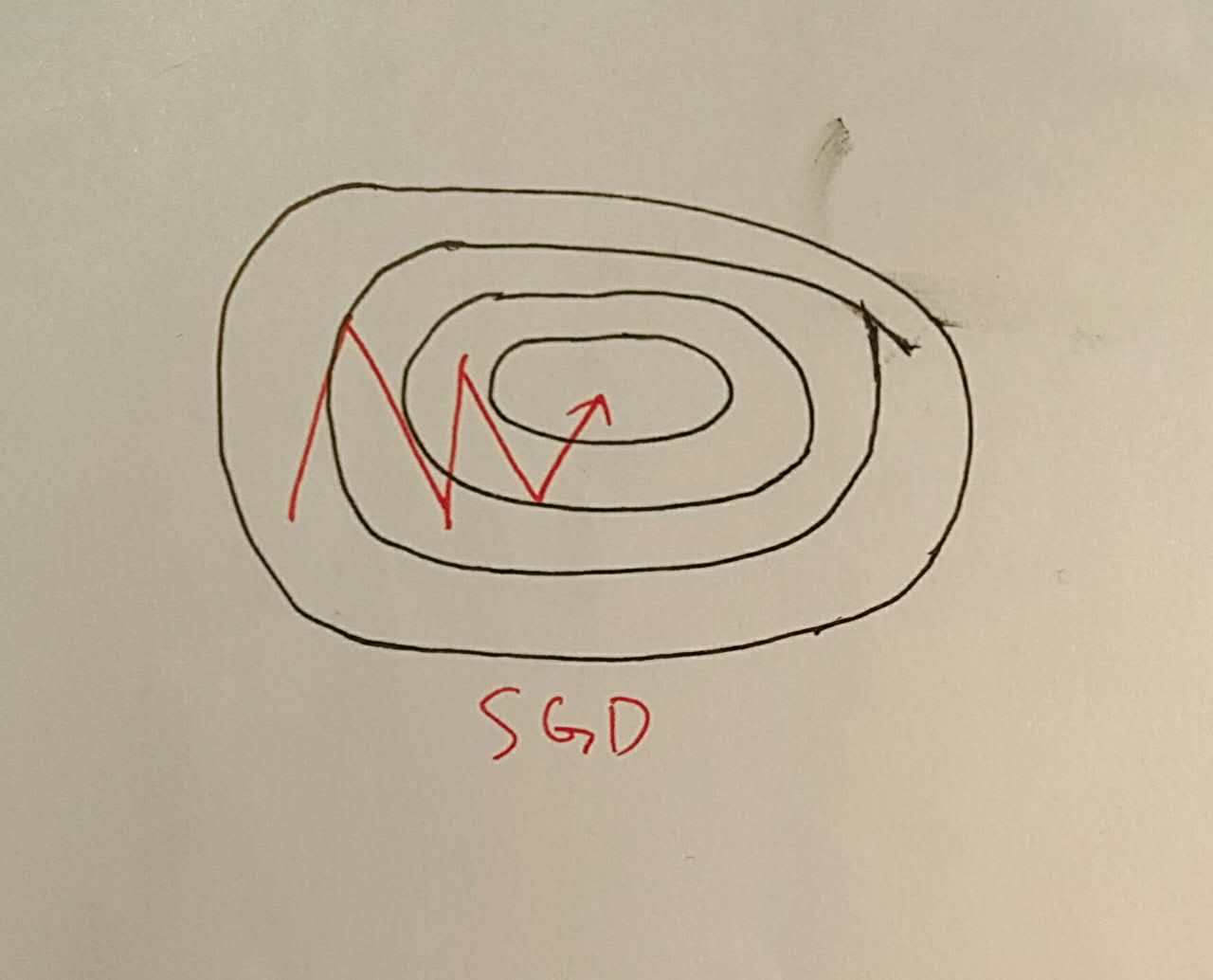
SGD with Momentum

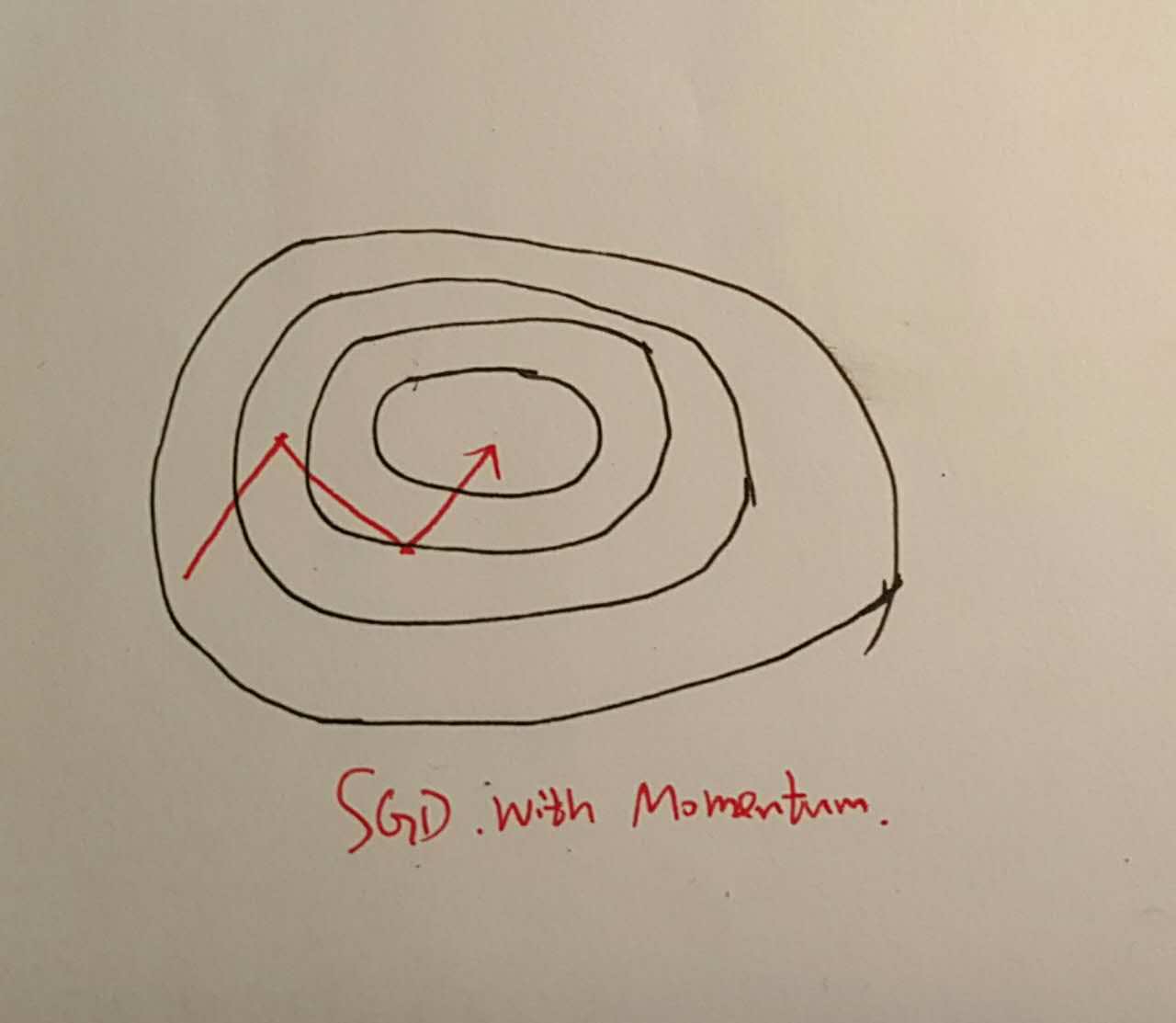
momentum的引入是为了一定程度上的解决上述的梯度波动问题，引入一个动量，每次首先去更新动量然后再去更新当前的参数，具体来说:

$v = mu * v - \alpha * dw$
$w += v$

上式看上去不太直观，但用直观的描述语言来说就是，我们每一次更新的时候都用上次的更新方向和这一次的负梯度方向进行相加。这样的好处是，如果它们方向相同，那么我们便可以加速该方向，如果方向不同，我们便进行中和，这相当于两个向量的加法的平行四边形法则。这样便能减少更新的波动并对更新进行加速。

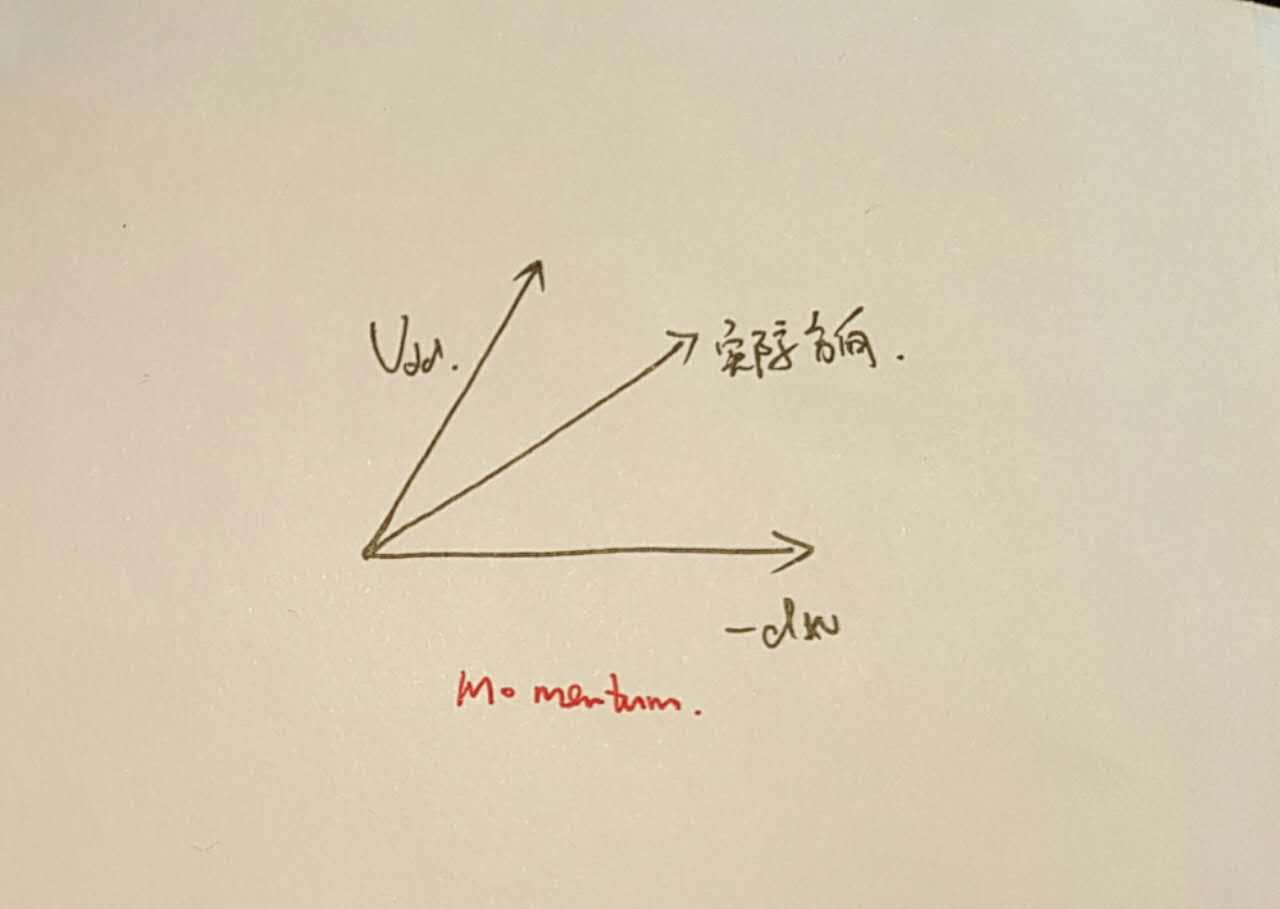
这样带来的好处是，我们可以减少波动，加速收敛。
sgdmomentum
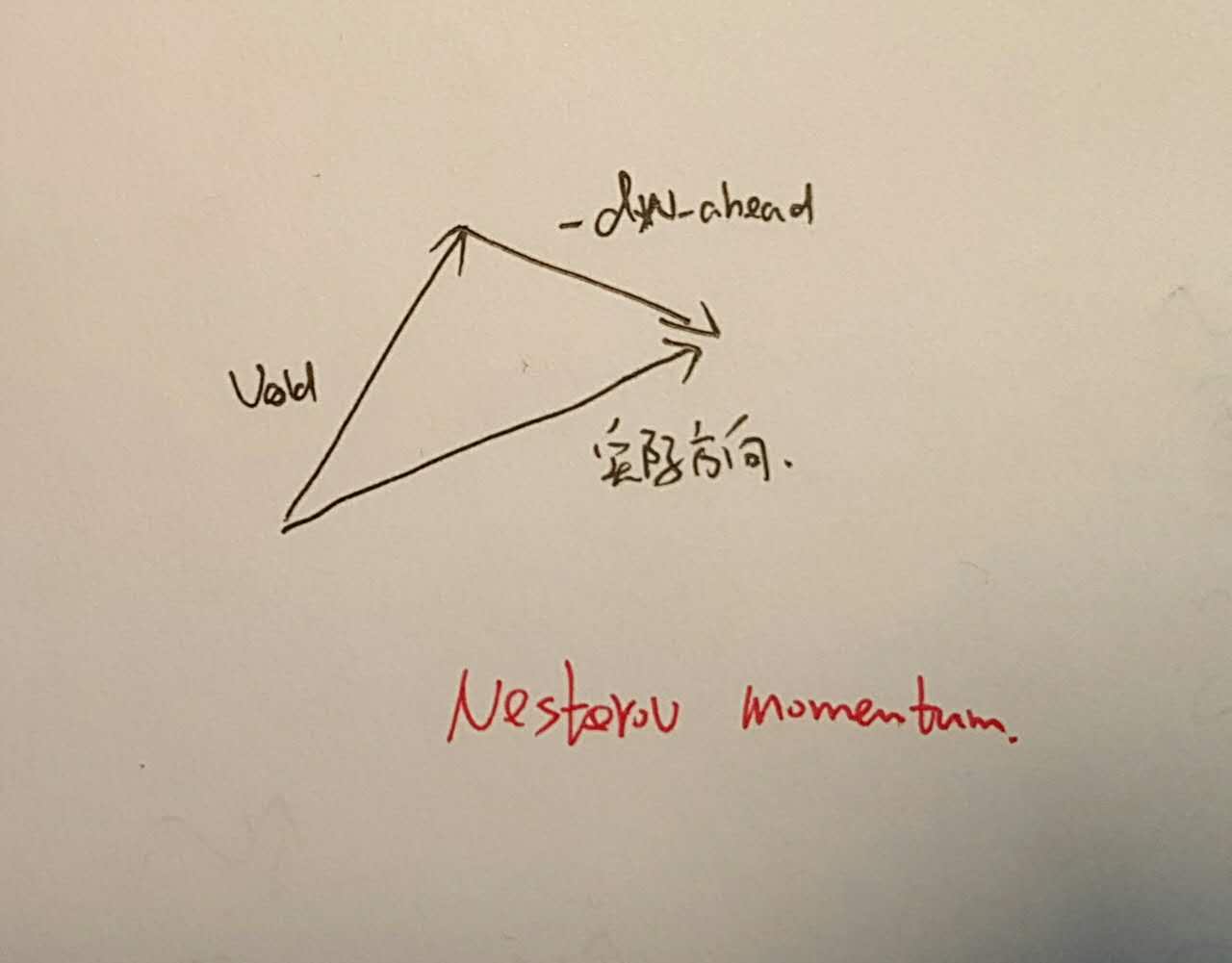
更进一步，我们干脆先在可能的位置进行gradient计算，而不是在当前位置计算，这叫做Nesterov Momentum，即:

$w_ahead = w + mu * v$
$v = mu * v - \alpha * dw_ahead$
$w += v$

还是在平行四边形上，其表现类似于:
Nesterov

$\alpha$学习速率的调节

前面我们的讨论中，对于所有的参数采用的都是同一个$\alpha$，需要我们手动的去调节$\alpha$，实际上在$\alpha$的调节上也有很多的工作。
Adagrad
Adagrad尝试着自动的去衰减学习速率$\alpha$，并且基于这样一个目的：梯度较大的应该拥有较小的学习速率，梯度较小的有较大的学习速率，尝试去平衡各参数的更新。具体来说:

$cache += dw^{2}$
$w += -\alpha * \frac{dw}{\sqrt{cache} + eps}$

即每次都去累计梯度的平方，然后实际更新的时候将学习速率除以该累计结果，导致的结果就是大梯度的学习速率会下降，而小梯度的学习速率会上升。但是该方法的一个致命缺点是学习速率下降过快，在没有达到最优前便使得$\alpha$几乎为0，停止学习。
RMSProp
RMSProp可以看做对于Adagrad太过激进的一个改进版本，引入了衰减系数，使得学习速率的衰减没那么快

$cache += decayrate * cache + (1 - decayrate) * dw^{2}$
$w += -\alpha * \frac{dw}{\sqrt{cache} + eps}$

Adam
Adam表现的有点像引入了momentum的RMSProp，不仅对$\alpha$进行累计衰减考虑，也对梯度进行相应的考虑

$cache1 += decayrate1 * cache1 + (1 - decayrate1) * dw^{2}$
$cache2 += decayrate2 * cache2 + (1 - decayrate2) * dw$
$w += -\alpha * \frac{cache2}{\sqrt{cache1} + eps}$

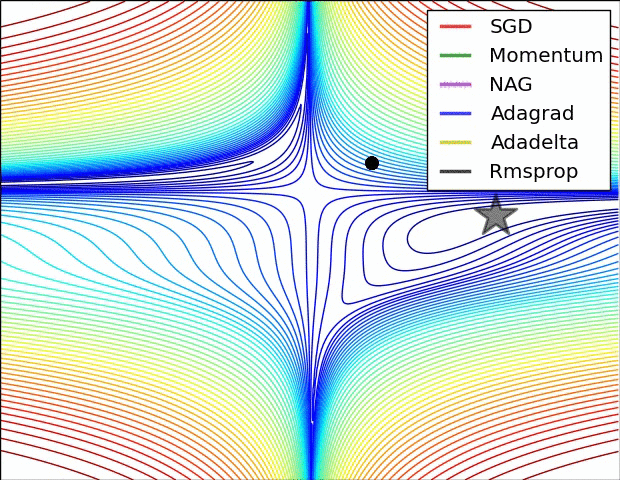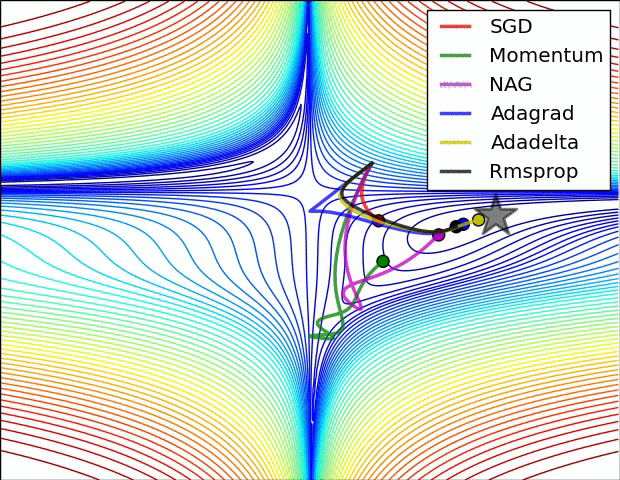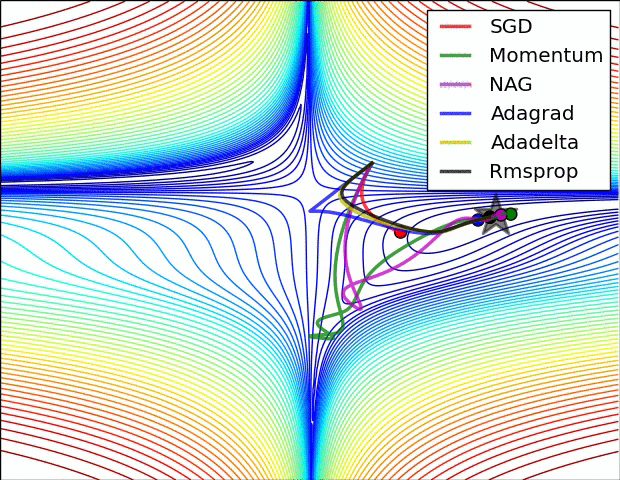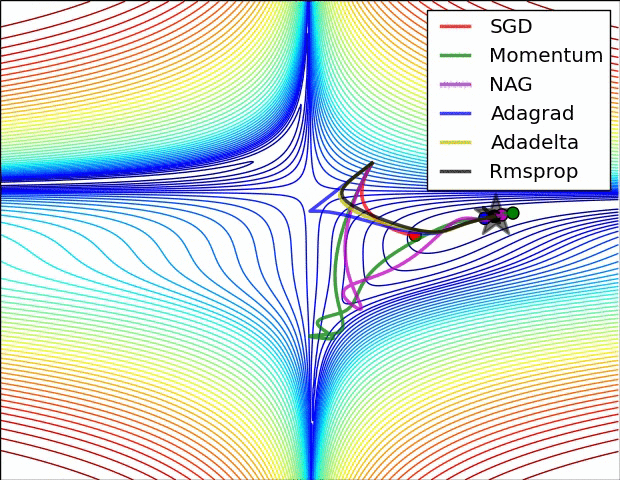
借用一个网上常见的优化方法图来表示，如下所示:
optimize