从最优化间隔器到核函数---SVM的推论（下）

Jan.30-2017

上文从最优化间隔器引入了线性可分支持向量机（硬间隔最大化）以及线性支持向量机（软间隔最大化），它们都只适用于数据的分隔面为线性的情况，当数据不是分隔时便不适用了。本文将先引入核函数的概念，它的引入可以使SVM的分类能力大大提高，甚至可以对无线维的数据进行分类。

一、核函数

回想一下我们在处理learning问题的时候，很可能不是直接使用输入特征$x$，而是对其进行一定的处理再使用，比如我们很可能使用$x^{2},x^{3}$等来获得一个新的特征。我们将原始的$x$称为输入空间，将这一变换过后的变量称为特征空间。这一变换过程我们可以用$\phi$来表示，我们称这一变换为特征变换。在这个例子中我们有:

$\phi(x) = \begin{bmatrix} x^{2} \\ x^{3}\end{bmatrix}$

大家可能有疑惑这个特征变换有什么用呢？特征变换最大的作用是我们可以将原本线性不可分数据经过变换后变得线性可分。考虑如下一个例子：

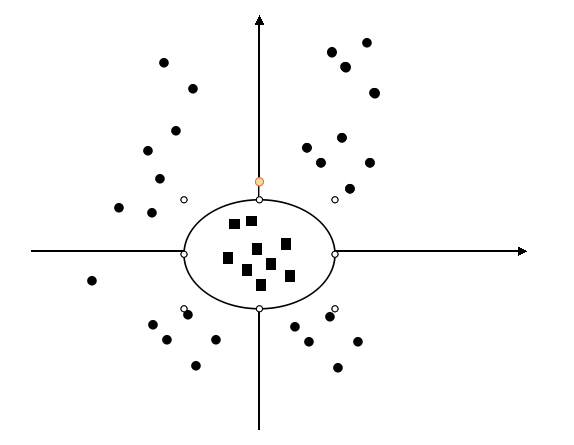
seperate

我们假设原输入空间$x \epsilon R^{2}$, $x=(x_1, x_2)$，如上图所示。显然在这个空间里两个类别是线性不可分的。但是如果我们定义一个映射:

$\phi(x) = \begin{bmatrix} x_1^{2} \\ x_2^{2}\end{bmatrix}$

我们称新的空间为$z \epsilon R^{2}$.显然在原空间中有:

$w_1x_1^{2} + w_2x_2^{2} + b = 0$

经过映射有：

$w_1z_1 + w_2z_2 + b = 0$

图像变为了：

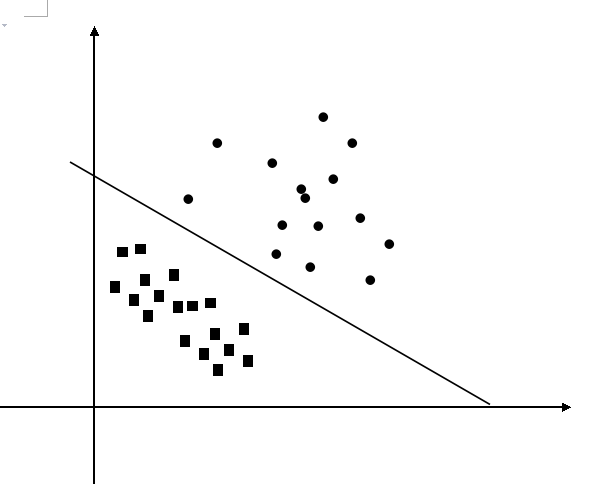
seperate2

显然经过变换后原来线性不可分的输入空间在特征空间中变得线性可分起来了。

以上直觉告诉我们，如果要利用线性分类方法来求解非线性问题的话我们可以：1、利用一个变换将原空间映射到新空间。2、在新空间中学习线性模型。

那么什么是核函数呢？
核函数的定义： 假设$\chi$是输入空间，又假设$\varphi$为特征空间，那么如果存在一个从$\chi$到$\varphi$的映射

$\phi(x):\chi \rightarrow \varphi$

对所有的都有$x_1,x_2 \epsilon \chi$，函数$K(x_1,x_2)$都满足条件:

$K(x_1,x_2) = \phi(x_1)^{T}\phi(x_2)$

那么称$K(x_1,x_2)$为核函数，$\phi(x)$为映射函数。

读者可能有疑问核函数有什么用呢？它和之前我们之前说的特征映射有什么关系呢？关键点在于：

显式的计算$\phi(x)$有时候是代价是很大的，这是因为很可能映射会存在于一个维度特别高的空间中，而利用核技巧，我们并不显式地定义映射$\phi$而是直接定义核函数$K(x,z)$，而核函数的计算往往是容易的

那么读者可能又会想了，核函数表示的是映射空间中的两个量的内积啊，应该怎么用呢？我们注意到在线性支持向量机的对偶形式中，优化问题由以下给出：

$W(\alpha)= \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i.x_j) - \sum_{i=1}^{m}\alpha_i$

可以看到该目标函数中的内积如果我们经过映射会变为$(\phi(x_i).\phi(x_j))$，而它正好可以用核函数来代替！此时我们优化目标变为了：

$W(\alpha)= \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_jk(x_i,k_j) - \sum_{i=1}^{m}\alpha_i$

可以看到，我们只需要定义核函数便可以隐式地将特征映射用上了。这等价于我们首先将原空间映射通过一个特征映射映射到新空间，然后在新空间中学习线性支持向量机。注意当映射函数是非线性时，我们学习到的便是非线性分类模型。

也就是说在核函数的条件下我们可以利用解线性分类问题的方法来求解非线性问题，我们利用核函数隐性地在特征空间中学习分类器，并不需要明确地去定义映射以及特征空间。这样的技巧称为核技巧，它是巧妙地利用线性分类学习方法与核函数来解决分线性问题的技巧。其实只要是有内积形式的优化问题都可以用上核技巧。

到这里读者又会有疑问了，既然不定义映射函数只定义核函数，那么我们怎么知道哪些核函数是有效的呢？即在不给定$\phi(x)$的情况下，我们怎么判断一个给定的函数$K(x,z)$是不是核函数？下面我们简单的给出一个定理并只给出直观的概念，关于严谨的证明读者可以参考相关的文献。

假设K是一个有效的核函数，对应于某个特征映射$\phi$,现在考虑含有m个点的有限集合，并且定义一个$m * m$的矩阵K，K的定义为$K_ij = K(x^i, x^j)$，这里K叫做核矩阵。注意到如果我们有一个有效的核函数，那么有

$K_ij = K(x^i,x^j) = \phi(x^i)^T\phi(x^j)=\phi(x^j)T\phi(x^i)=K(x^j, x^i)=K_ji$

也就是说K必然是一个对称矩阵，更进一步，我们令$\phi_k(x)$表示$\phi(x)$的第$k$项，对于任意向量$z$有：

$z^TKz = \sum_i\sum_jz_iK_ijz_j$ $=\sum_i\sum_jz_i\phi(x^i)T\phi(x^j)z_j$ $=\sum_i\sum_jzi\sum_k\phi_k(x^i)\phi_k(x^j)z_j$ $=\sum_k\sum_i\sum_jz_i\phi_k(x^i)\phi_k(x^j)z_j$ $=\sum_k(\sum_iz_i\phi_k(x^i))^2$ $\geq 0$

说明了矩阵K还必须是半正定的。

由上面的例子我们说明了，如果K是有效的核函数，那么其对应的核矩阵$K \epsilon R^{m\times m}$必然是对称半正定的。其实该条件不仅是有效核函数的一个必要条件也是一个充分条件。这就是有名的Mercer定理。

Mercer定理. 假设K是一个$R^n \times R^n \rightarrow R$的函数映射，那么K为有效(Mercer)核的充要条件是对于任意的数据集${x^i,…,x^m}, m < \infty$，其对应的核矩阵为对称半正定。

根据Mercer定理我们就可以很方便快捷得确定一个函数到底是不是有效核。

至此我们可以完整的引入了核技巧。核技巧的引入使得我们得以处理高维空间中的分类问题，将SVM的应用范围大大的拓展开来。值得注意的是，核技巧的应用远不止SVM中，一个算法如果可以写成$(x^i,x^j)$的形式那么我们便可以将核技巧应用上去，比如说可以有基于核技巧的Logistic Regression等。

二、SVM的实现—SMO算法

要引入SMO算法首先来了解下坐标上升法，对于一个不带约束的优化问题：

$maxW(\alpha_1, \alpha_2, ..., \alpha_m)$

我们循环地对每个变量进行优化，直到最终收敛，即：
Loop until convergence: { For i = 1,…, m { $\alpha_i := \arg\max_\alpha W(\alpha_1,\alpha_{i-1},..., \alpha_m)$ }} 即每次我们都固定其它变量，只对一个变量进行最优化求解，直到最终收敛。注意到在坐标上升法中，由于每次都只优化一个变量，所以轨迹图是始终平行于坐标轴的。一个类似的函数图如下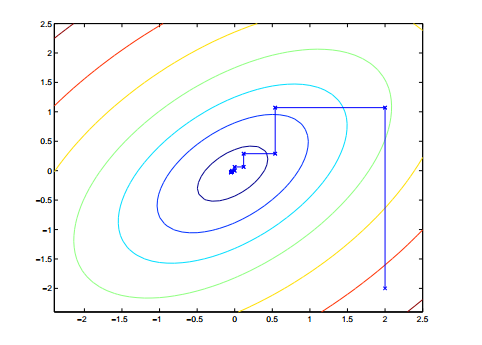： accord_ascend SMO算法的思路来源于此。关于SMO算法的具体思路以后将结合代码具体讲解。